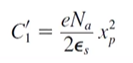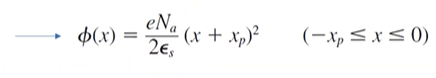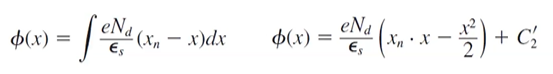Semiconductor - Ch7-1(4) / Zero Applied Bias / Electric Potential / Space Charge Width
Electric Potential
Electric Potential과 Electric Field의 관계
전자기학에서 가장 기본적으로 다루었던 이야기이다. (Ch4,Ch6)
E-field를 적분한 것의 음수가 Electric Potnetial이 된다.
E-field를 통해 E-Potential 계산
[In the P region]
적분을 하면 적분 상수가 생기므로 Boundary Condition을 통해 적분상수를 계산해야 E-potential 식이 완성된다.
,. Boundary Condition을 대입해서 계산하면 적분상수가 아래와 같이 나온다.
p region에서의 Electric Potential의 식은 다음과 같다.
그래프로 나타내었을 때 그 기울기는 제곱으로 증가하고 있다. (아래에서 다시 설명 )
[In the n region]
위 식 역시 Boundary Condition 대입을 통해 적분 상수 계산이 필요하다.
n region영역에 대한 Electric Potentail을 계산할 때에는 p region과 달리 연속성을 이용한
위 식을 Boundary Condition으로 하여 계산한다.
n region의 electric potential의 최종 식은 위와 같다.
[연속성]
Electirc-field 뿐만 아니라, Electric Potential에서도 마찬가지로 연속성이 적용된다.

p region의 electric potentail과 n region의 electric poetential은 접합면인 x=0의 지점에서 같은 값을 가져야한다.
Electric potential ( built-in potential )
Electric potetnail through the space charge region of a uniformly doped pn junction
거리 x에 따라 전위를 봤을 때,
-Xp까지는 전위가 0이고, space charge region내에서
위치가 Xn이 될 때까지 전위가 상승한다.
(x=Xn)에서의 전위값(electric potential)이 바로 built-in potential이며,
Xn이상부터는 built-in potential의 값으로 전위값이 유지된다.
아래는 built-in potentail 계산 식이다.
built_in potential(Vbi)통해 xp와 xn을 구할 수 있게 된다.
따라서 W(Space charge width)도 구할 수 있게 된다. ( W = |Xp| + Xn )
Space Charge Width
Xn, Xp 구하기
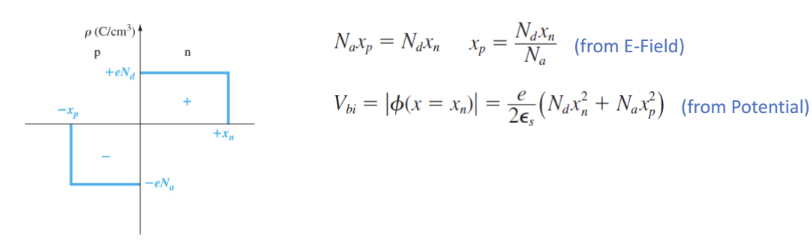
앞선 글에서 설명하였던 E-field와 위에서 설명하였던 potential에 대한 두 식을 통해
Vbi에 대한 위 식을 Xn을 구하기 위한 식으로 정리하면(Xp는 E-field에 있는 것 대입)
아래와 같이 식이 정리된다.
| Xn ( n region ) | Xp ( p region ) |
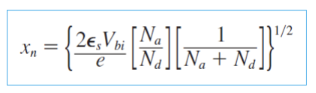 |
 |
따라서 Xn,Xp는 모두 Na와 Nd를 이용하여 구할 수 있고,
식 내부에 있는 Vbi(built_in potential) 도 두 농도를 통해 구할 수 있다.
즉 p,n type의 농도가 구해졌을 때 농도를 통해 Vbi를 구하고, Xn, Xp까지 구할 수 있게 된다.
Space charge region (width) 구하기
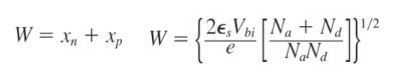
Xn과 Xp를 통해 최종적으로 space charge width를 구할 수 있게 된다.
Xn과 Xp를 더해서 구하면 위와 같이 식이 간단히 정리된다.